Relevanz im Lehrplan
Gymnasium
:
12. Jahrgangsstufe
FOS
:
11. Jahrgangsstufe Nichttechnik, 13. Jahrgangsstufe Technik
BOS
:
12. Jahrgangsstufe Technik, 13. Jahrgangsstufe Nichttechnik
Vorgesehenes Vorgehen:
- Schauen Sie sich das Video aufmerksam an.
- Bearbeiten Sie dann das Skript sorgfältig.
- Bei Verständnisproblemen rufen Sie die entsprechende Stelle des Videos nochmal auf.
Skript wird nicht geladen? -> Bitte im Feld rechtsklicken und auf „Frame neu laden“ klicken oder +- auswählen.
Skript wird nicht geladen? -> Bitte im Feld rechtsklicken und auf „Frame neu laden“ klicken oder +- auswählen.
Skript wird nicht geladen? -> Bitte im Feld rechtsklicken und auf „Frame neu laden“ klicken oder +- auswählen.
Skript wird nicht geladen? -> Bitte im Feld rechtsklicken und auf „Frame neu laden“ klicken oder +- auswählen.
Skript wird nicht geladen? -> Bitte im Feld rechtsklicken und auf „Frame neu laden“ klicken oder +- auswählen.
Formelsammlung
Merke: Aus einer Urne mit n unterscheidbaren Kugeln werden nacheinander k Kugeln
mit Berücksichtigung der Reihenfolge und mit Zurücklegen gezogen. Dafür gibt es
|Ω|=nk
verschiedene Möglichkeiten.
.
Merke: Aus einer Urne mit n unterscheidbaren Kugeln werden nacheinander k Kugeln
mit Berücksichtigung der Reihenfolge und ohne Zurücklegen gezogen. Dafür gibt es
|Ω|=n⋅(n−1)⋅(n−2)⋅…⋅(n−k+2)⋅(n−k+1)=n!(n−k)!..
verschiedene Ergebnisse.
.
Merke: Aus einer Urne mit n unterscheidbaren Kugeln werden nacheinander k Kugeln
ohne Berücksichtigung der Reihenfolge und ohne Zurücklegen gezogen. Dafür gibt es
|Ω|=n!(n−k)!k!..=(.n..k.) (Sprich: “n über k“)
viele Möglichkeiten.
.
Merke: Aus einer Urne mit n unterscheidbaren Kugeln werden nacheinander k Kugeln
mit Berücksichtigung der Reihenfolge und mit Zurücklegen gezogen. Dafür gibt es
|Ω|=(.n+k−1..k.)
verschiedene Möglichkeiten.
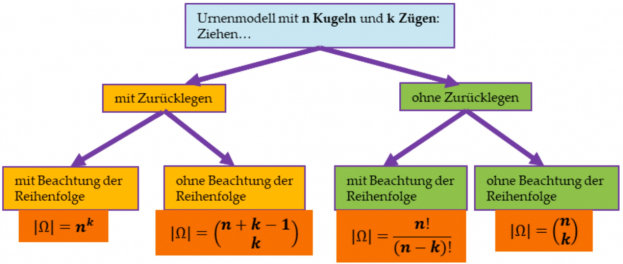
5.3.5 Zusammenfassung, Übung, Anwendung
.
.
Merke: Permutation
Werden aus einer Urne mit n unterscheidbaren Kugeln alle Kugeln
ohne Zurücklegen und mit Berücksichtigung der Reihenfolge gezogen, dann gibt es
|Ω|=n!
viele Kombinationen.
.
Merke: Permutation mit Wiederholung
In einer Urne mit n Kugeln befinden sich jeweils km (m∈N) gleiche Kugeln. Werden alle Kugeln
ohne Berücksichtigung der Reihenfolge und ohne Zurücklegen gezogen, dann gibt es dafür
|Ω|=n!k1!⋅k2!⋅k3!⋅…⋅km!..
mögliche Kombinationen..